A recurring strand in Exeter's math curriculum
Mathematical models arise in a variety of settings throughout our problem sets. Here are a few examples.
Math 1: Chris does a lot of babysitting. When parents drop off their children and Chris can supervise them at home, the hourly rate is $3. If Chris has to travel to the child’s home, there is a fixed charge of $5 for transportation in addition to the $3 hourly rate.
- Graph y = 3x and y = 3x + 5. What do these lines have to do with the babysitting context? What feature do they have in common? How do they differ?
- What does the graph of y = 3x + 6 look like? What change in the babysitting context does this line suggest?
(Math 1, #193)
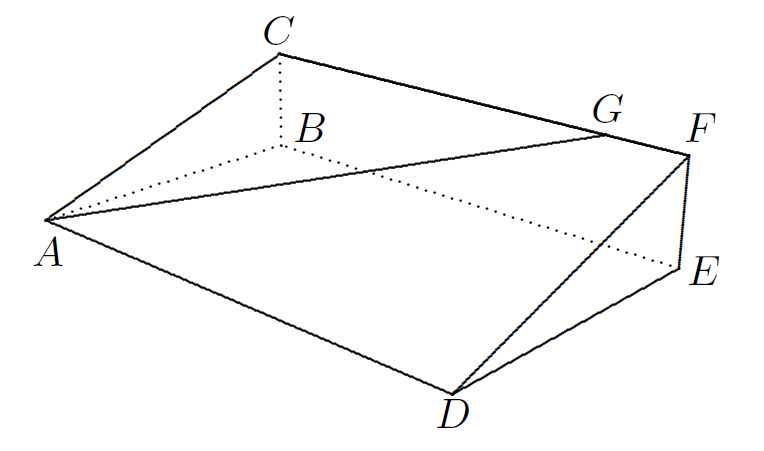
(Math 2, 75#9)
Math 3: Suppose that three PEA students know a certain rumor at noon, that there are 1000 students in all, and that any student will try to pass a rumor along to one more student each hour. This suggests the model , where is the number of students who know the rumor hours after noon. It is given that = 3. The fraction in the recursive equation represents that portion of the student body that does not know the rumor. Calculate , , and . Your answers will suggest the equation , which describes 100% growth. Explain why this model becomes less realistic as n increases.
(Math 3, 77#3)
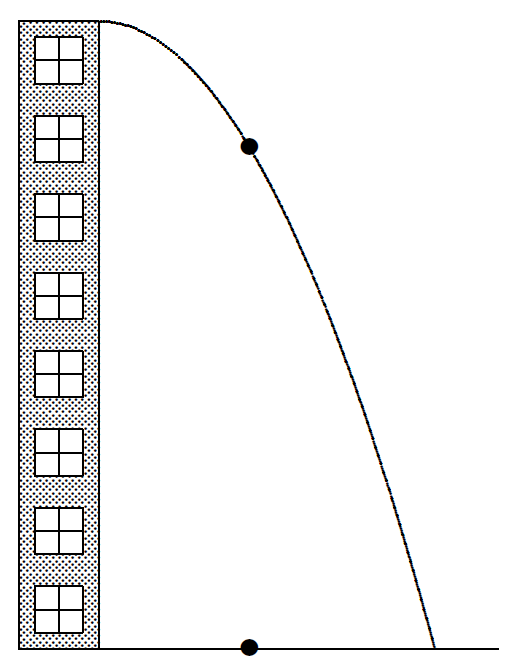
When t = 1, how fast is the shadow moving? How fast is the projectile losing altitude? How fast is the projectile moving?
What is the altitude of the projectile when t = 2? What is the altitude of the projectile a little later, when t = 2 + k? How much altitude is lost during this k-second interval? At what rate is the projectile losing altitude during this interval?
(Math 4, 11#6)
Other strands that arise throughout our problem sets: