A recurring strand in Exeter's math curriculum
Optimization problems arise in a variety of settings throughout our problems sets. Here are a few examples.
Math 1: Robin works part-time carving wooden seagulls and lobsters to sell to tourists during the summer season. Keeping up with demand means carving at least two seagulls and three lobsters a day. Robin can produce at most a dozen models a day. Can Robin make a profit of $70 in one day? What combination of seagulls and lobsters produces the greatest daily profit? What is this maximum profit?
(Math 1, #566)
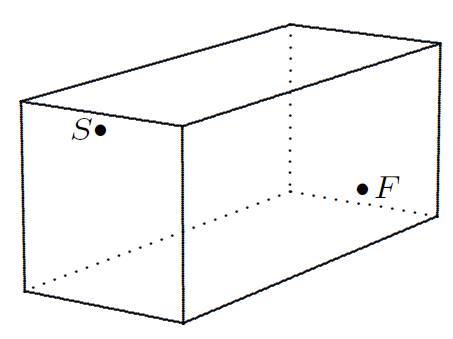
(Math 2, 24#2)
Math 3: The diameter and the slant height of a cone are both 24 cm. Find the radius of the largest sphere that can be placed inside the cone. (The sphere is therefore tangent to the base of the cone.) The sphere occupies a certain percentage of the cone’s volume. First estimate this percentage, then calculate it.
(Math 3, 29#5)
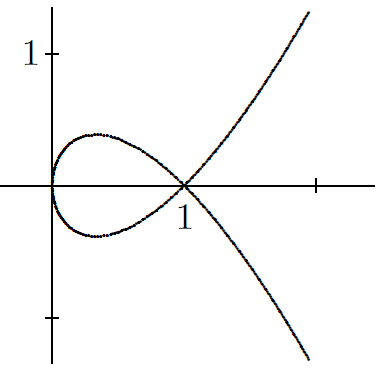
(Math 4, 62#8, image from 62#3)