Rates of change arise in a variety of settings throughout our problem sets. Here are a few examples.
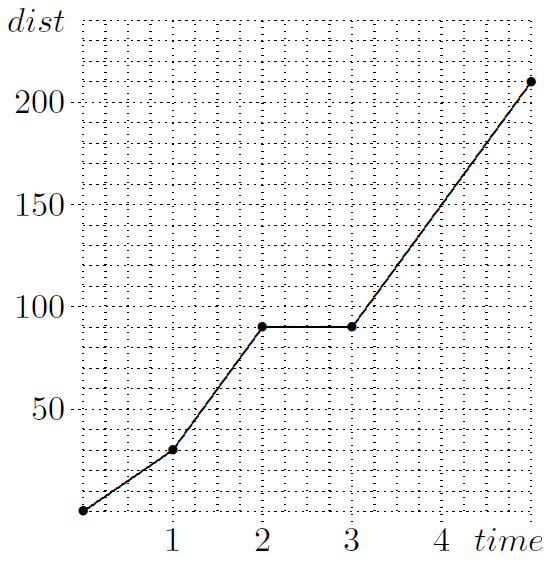 Math 1: Sandy recently made a 210-mile car trip, starting from home at noon. The graph at right shows how Sandy’s distance from home (measured in miles) depends on the number of hours after noon. Make up a story that accounts for the four distinct parts of the graph. In particular, identify the speed at which Sandy spent most of the afternoon driving.
Math 1: Sandy recently made a 210-mile car trip, starting from home at noon. The graph at right shows how Sandy’s distance from home (measured in miles) depends on the number of hours after noon. Make up a story that accounts for the four distinct parts of the graph. In particular, identify the speed at which Sandy spent most of the afternoon driving.
(Math 1, #143)
Math 2: An Unidentified Flying Object (UFO) moving along a line with constant speed was sighted at (8, 9, 10) at noon and at (13, 19, 20) at 1:00 pm. Where was the UFO at 12:20 pm? When, and from where, did it leave the ground (z = 0)? What was the UFO’s speed?
(Math2, 37#6)
Math 3: A spherical balloon is being inflated by a machine that increases the balloon’s volume at a steady 1000 cc per second.
Show that the balloon’s radius after 6.0 sec of inflation is approximately 11.273 cm.
What is the balloon’s radius after 6.1 sec of inflation?
Find approximately the rate (cm/sec) at which the radius is increasing at that instant when the volume reaches 6000 cc.
(Math3, 54#8)
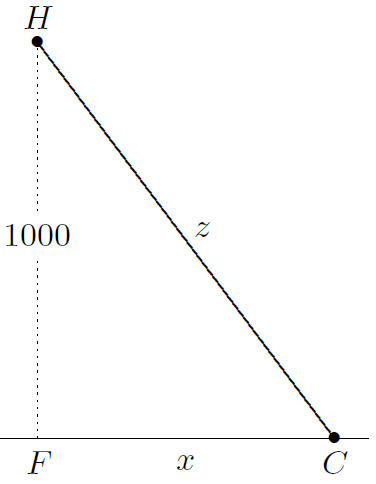 Math 4: A police helicopter H is hovering 1000 feet above a highway, using radar to check the speed of a red convertible C below. The radar shows that distance HC is 1250 feet and increasing at 66 feet per second. The obvious question: Is the car exceeding the speed limit, which is 65 mph? Here is how to figure out the speed of the car: Let x = FC, where F is the point on the highway that is directly beneath H, and let z = HC. Notice that x and z are both functions of t, and that z(t)2 = 10002 + x(t)2 . Differentiate both sides of this equation with respect to t. The new equation involves dx/dt and dz/dt as well as x and z. The radar shows that dz/dt = 66 when z = 1250. Use this data to calculate dx/dt.
Math 4: A police helicopter H is hovering 1000 feet above a highway, using radar to check the speed of a red convertible C below. The radar shows that distance HC is 1250 feet and increasing at 66 feet per second. The obvious question: Is the car exceeding the speed limit, which is 65 mph? Here is how to figure out the speed of the car: Let x = FC, where F is the point on the highway that is directly beneath H, and let z = HC. Notice that x and z are both functions of t, and that z(t)2 = 10002 + x(t)2 . Differentiate both sides of this equation with respect to t. The new equation involves dx/dt and dz/dt as well as x and z. The radar shows that dz/dt = 66 when z = 1250. Use this data to calculate dx/dt.
(Math 4, 48#6)
Other strands that arise throughout our problem sets:

