A recurring strand in Exeter's math curriculum
Symmetry arises in a variety of settings throughout our problem sets. Here are a few examples.
Math 1: A hot-air balloon ride has been set up so that a paying customer is carried straight up at 50 feet per minute for ten minutes and then immediately brought back to the ground at the same rate. The whole ride lasts twenty minutes. Let h be the height of the balloon (in feet) and t be the number of minutes since the ride began. Draw a graph of h versus t. What are the coordinates of the vertex? Find an equation that expresses h in terms of t.
(Math 1, #376)
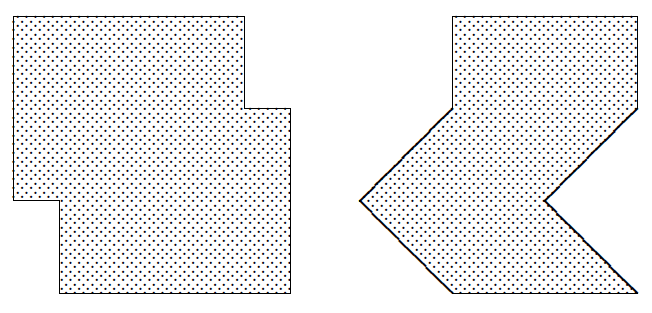
Math 2: Find as many ways as you can to dissect each figure at right into two congruent parts.
(Math 2, 6#10)
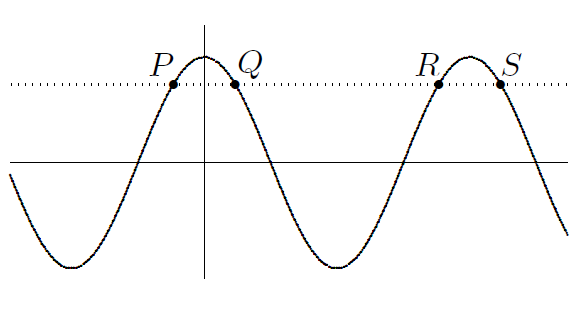
(Math 3, 19#4)
Math 4: Given that function f has the property f(180 − x) = f(x) for all x-values, show that the graph y = f(x) has reflective symmetry. Identify the mirror. Name two such functions.
(Math 4, 4#6)
Other strands that arise throughout our problem sets: