A recurring strand in Exeter's math curriculum
Transformations arise in a variety of settings throughout our problem sets. Here are a few examples.
Math 1: Graph y = |x−5| and y = |x+3|, then describe in general terms how the graph of y = |x| is transformed to produce the graph of y = |x−h|.
(Math 1, #309)
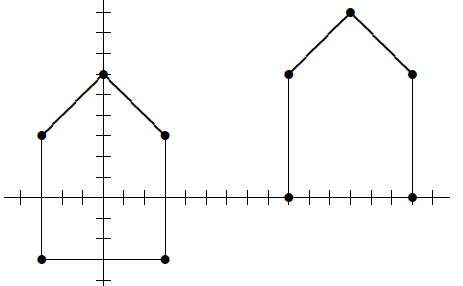
- vertices (3, −3), (3, 3), (0, 6), (−3, 3), and (−3, −3);
- vertices (15, 0), (15, 6), (12, 9), (9, 6), and (9, 0). Are the results what you expected?
(Math 2, 54#6)
Math 3: Describe the effect of each of the following geometric transformations. To generate and test your hypotheses, transform some simple points.
(a) T(x,y) = (−3x, −3y)
(b) T(x,y) = (−y,x)
(c) T(x,y) = (−y, −x)
(d) T(x,y) = (0.6x− 0.8y, 0.8x+ 0.6y)
(Math 3, 16#6)
Math 4: The slope of the curve y= 2x at its y-intercept is ln(2), which is approximately 0.693. Use this information (but no calculator) to find the slope of the curve y= 3 2x at its y-intercept. Answer the same question for y= 23 2x, then use your result to find the slope of the curve y= 2x at the point (3, 8).
(Math 4, 20#6)
Other strands that arise throughout our problem sets: