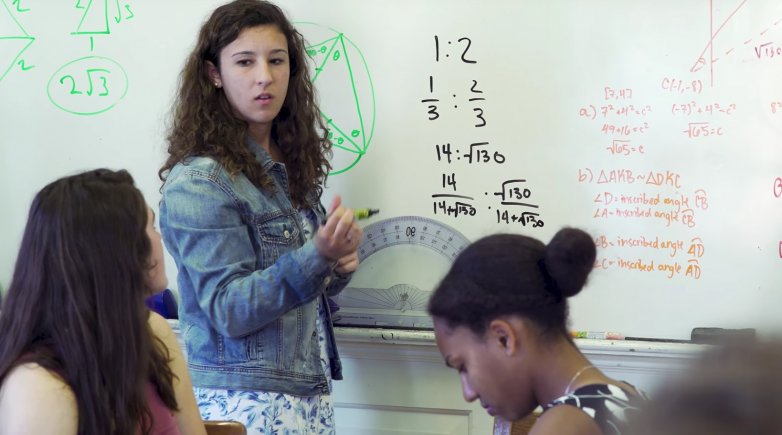Without the contextual clues, students must call on all the math they’ve learned through the term and over the years, not just from that day’s lesson and not just to heed a teacher’s prompt. The idea echoes “Pascal’s Method.” The 17th-century French philosopher argued that “people are generally better persuaded by the reasons which they have themselves discovered than by those which have come into the mind of others.”
The Harkness table has proved to be the perfect arena for this approach. Students dig into the material before class, then sort through their work together, bouncing ideas off one another and often winding up in a very different place from where they began.
“When I do math now, I do it without any prejudice,” says Jack Liu ’20, who is early into a two-term sequence of Math 610: Multivariable Calculus. “I don’t really think about whether this is a hard problem or an easy problem. I think about attacking it holistically, trying not to make any presumptions, trying not to jump to the answer. To really feel out the math, and be creative with it.”
That is precisely the point. Math is like an art form, and just as in art class, the idea is to develop an environment in which students’ creativity is fostered. Students figure out the rules on their own and apply those rules as they see fit.
Work in progress
The problem sets have become Exeter vernacular. Every student studies them. By the end of prep year, students are as familiar with the recurring character “Alex the geologist” as they are with their roommates.
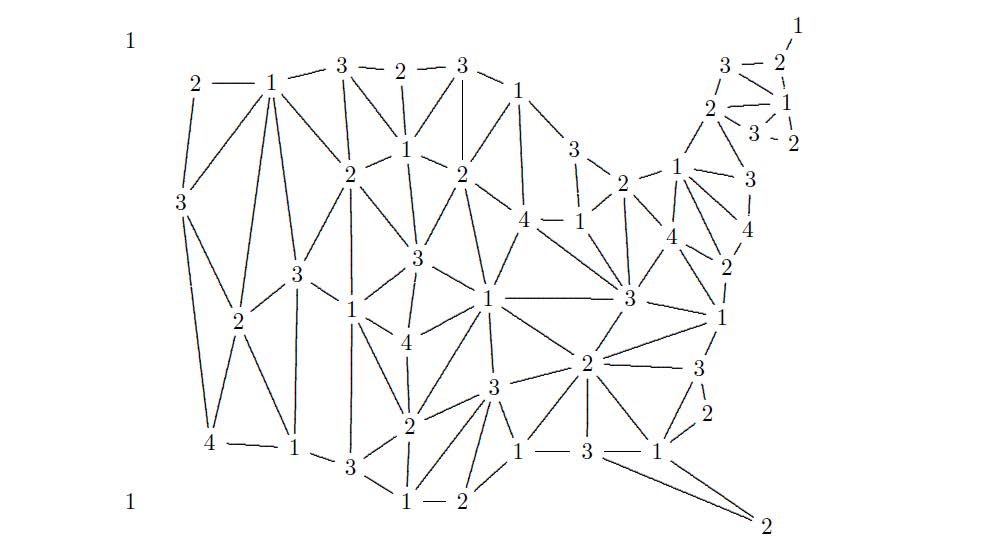
But the sets are not dogma. The work Parris and company spearheaded nearly three decades ago was the foundation, but the house is never finished. Problems evolve as new paths to an outcome are discovered. Problem No. 155 in the Math 2 sets is a good example. Through the years, students from the classes of 2005, 2016 and 2019 have come up with viable solutions, as has a math teacher in Cleveland and a student in Chicago (the sets are published online). Each of these approaches was vetted by the math faculty at the conclusion of the school year and, once it passed muster, was added to the “commentary,” or teachers’ notes.
Last summer, several members of the math faculty gathered in Room 108 — Geer’s classroom — in the Academy Building to vet the recommendations and make the updates. Visitors to Room 108 are greeted by a cartoon from The New Yorker on the classroom door. In it, a group of lab-coated academics cower from a colleague gone mad above the caption, “Give him whatever he wants! He’s threatening to divide by zero!” It is an early giveaway that math happens there.
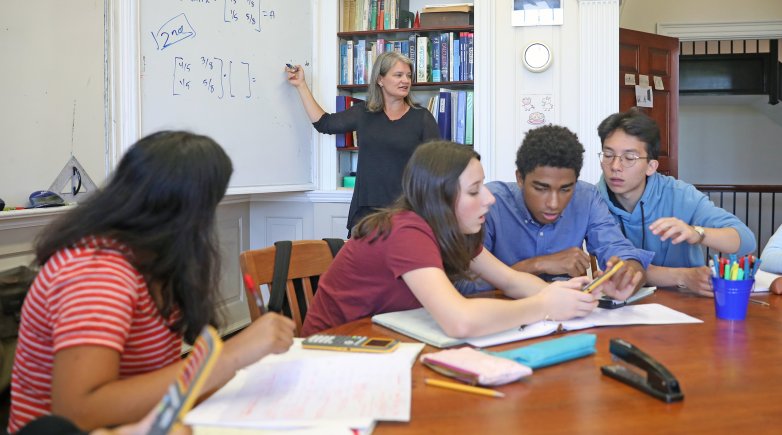





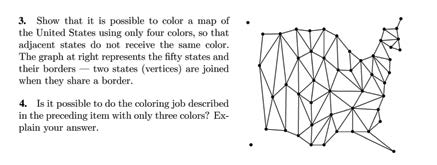



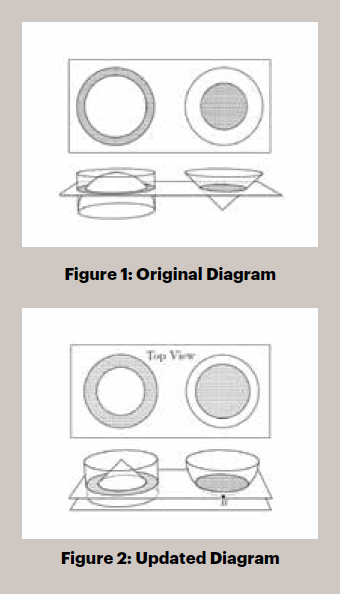 Exeter’s math problem sets are never complete. Each year, the math faculty reviews the 3,700-plus problems and makes modifications as needed. We asked Math Instructor Panama Geer to walk us through how a problem evolved over time:
Exeter’s math problem sets are never complete. Each year, the math faculty reviews the 3,700-plus problems and makes modifications as needed. We asked Math Instructor Panama Geer to walk us through how a problem evolved over time: